Philosophy

The philosophy of PRISM is to aide the user in understanding their own math models.

Math models can be small or large, and PRISM acts to parametrically drive them in order to reveal their properties.

Similar to high-end systems such as ModelCenter, PRISM aids in the design and optimization of systems. PRISM enables easy optimization, sensitivity study, and visualization.

A problem is defined by input and output parameters and those parameters are connected to the overall math model.

Results are presented as an assortment of graphs, charts, and images that convey insight into system trends, sensitivities, variations, and characteristics.

Output is generated in plain text, HTML, and native Microsoft Suite files (Excel, Word and PowerPoint). All of the above formats support conversion to PDF.

While PRISM can work with math models of any scientific or engineering discipline, its origins are in the aerospace, rocket propulsion industry and was originally created to aide in the understanding of those types of models. It operates with some aerospace standard support codes such as:

• CEA - Chemical Equilibrium With Applications
• RPA - Rocket Propulsion Analysis
• TDK - Two-Dimensional Kinetics Nozzle Performance (commercial)
• RefProp - Reference Fluid Thermodynamic and Transport Properties (commercial)

PRISM is written in the open source programming language python 2.7 and includes other open source codes

• POV-Ray - Persistence Of Vision Ray Tracing Program
• SciPy - Scientific Computing Library
• numpy - Numerical Python N-dimensional array package
• matplotlib - Comprehensive 2D Plotting

PRISM includes methods taken from ELES (Expanded Liquid Engine Simulation Computer Code)

created for AFRPL in 1985 under contract AFRPL-TR-85-055:

• ELES Technical Information Manual
• ELES New Users Manual
• ELES Advanced Users Manual
• ELES Solid GG Design Guide
• ELES Programmers Manual

Building Blocks

PRISM was created to conduct "full-up" analyses of propulsion systems, however, by its nature it also contains the building blocks to conduct smaller, more focused tasks.

Those building blocks are available to:

• Calculate Isp (TDK, CEA or RPA)
• Use Gas or Liquid Properties (RefProp, 1st Principles)
• Interpolate Data (linear, quadratic, cubic, other)
• Calculate Pressure Drops (Moody Chart)
• Optimize Something (Isp, Delta V, Mass, etc.)
• Solve ODE Initial Value (Hover Test, Detailed Pressurization)
• Size Engines, Tanks, Lines, Blowdown etc.
• Visualize Design Space
• Create Publication-Quality Results
• Convince Others That We Did Something Right

A number of small scripts are provided to to illustrate these tasks on the Building Blocks page of this document.

Math Models

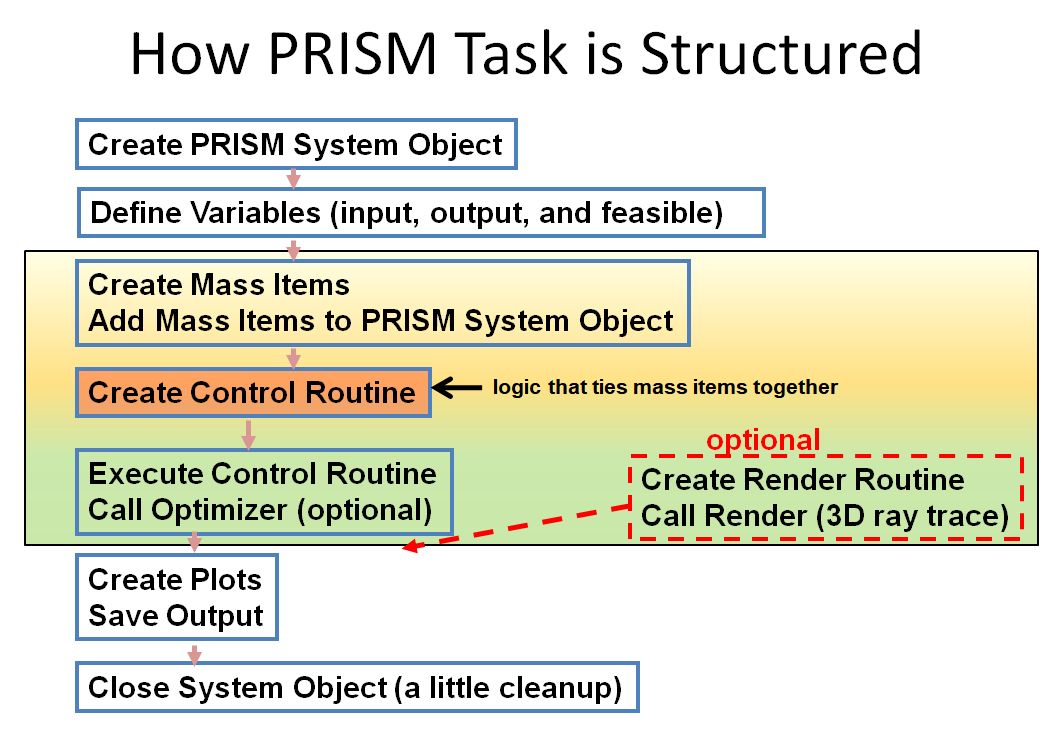
When a more complex model is required than just the straightforward use of a building block, a complete math model is constructed. The flow of the math model is described in the diagram below.

The Math Model page of this document, describes the steps required to build a math model.